seed 🌰
Mersenne’s Twister is unfortunately not a boogie-woogie dance, but fortunately is an interesting pseudo-random number generator (PRNG). I’ve never really looked into how random generators work and when seeing it come up in deck-shuffling code, thought it would be a good opportunity to look into the theory behind random number generation.
sapling 🌱
To understand the Mersenne Twister, I first checked the one and only Wikipedia. Here’s an exerpt:
“The Mersenne Twister algorithm is based on a matrix linear recurrence over a finite binary field. The algorithm is a twisted generalised feedback shift register (twisted GFSR, or TGFSR) of rational normal form (TGFSR(R)), with state bit reflection and tempering.”
I interpreted this as
“The Mersenne Twister algorithm ⏁⊑⟒ ⋔⟒⍀⌇⟒⋏⋏⟒. The algorithm ⏁⍙⟟⌇⏁⟒⍀ form ⏃⌰☌⍜⍀⟟⏁⊑⋔ ⟟⌇ ⏚⏃⌇⟒⎅ ⍜⋏.”
Alright, try number two. The Mersenne Twister is based on repeated matrix operations in the binary field (1 or 0 with binary math – just think everything mod 2). The algorithm takes the binary representation of an initial seed number and manipulates (shifts) the bits of the register based on input from the last shifted bits (takes in feedback from last shift and uses it to determine new shift). With this linear recurrence, we can define a series. Each number in the series is then put through a tempering matrix that again alters the bits so that it makes the distribution less predictable.
tree 🌳
Let’s take a closer look at the recurrence relation. The series, as defined in Wikipedia, can be hard to interpret, so let’s start with a quite literally Nibble-sized example. Assume we have a small word size of 4 bits. Let’s say our original state vector is, for example, \( x_0 = 1010 \) and \( x_1 = 1100 \). We define \( u = 2 \) and \( l = 2 \) as the bit shifts. The operation \( x_k^u \) shifts \( x_k \) to the right by \( u \) bits, resulting in \( x_0^u = 10 \). Similarly, the operation \( x_{k+1}^l \) shifts \( x_{k+1} \) to the left by \( l \) bits, yielding \( x_1^l = 00 \). Concatenating these values (using the | operation), we get \( 1000 \). If we define a matrix \( A \) to perform a simple XOR operation, then we find that \( x_{k+n} = 1000 \oplus 0111 = 1111 \). This example is highly simplified, but it captures the fundamental principles at play.
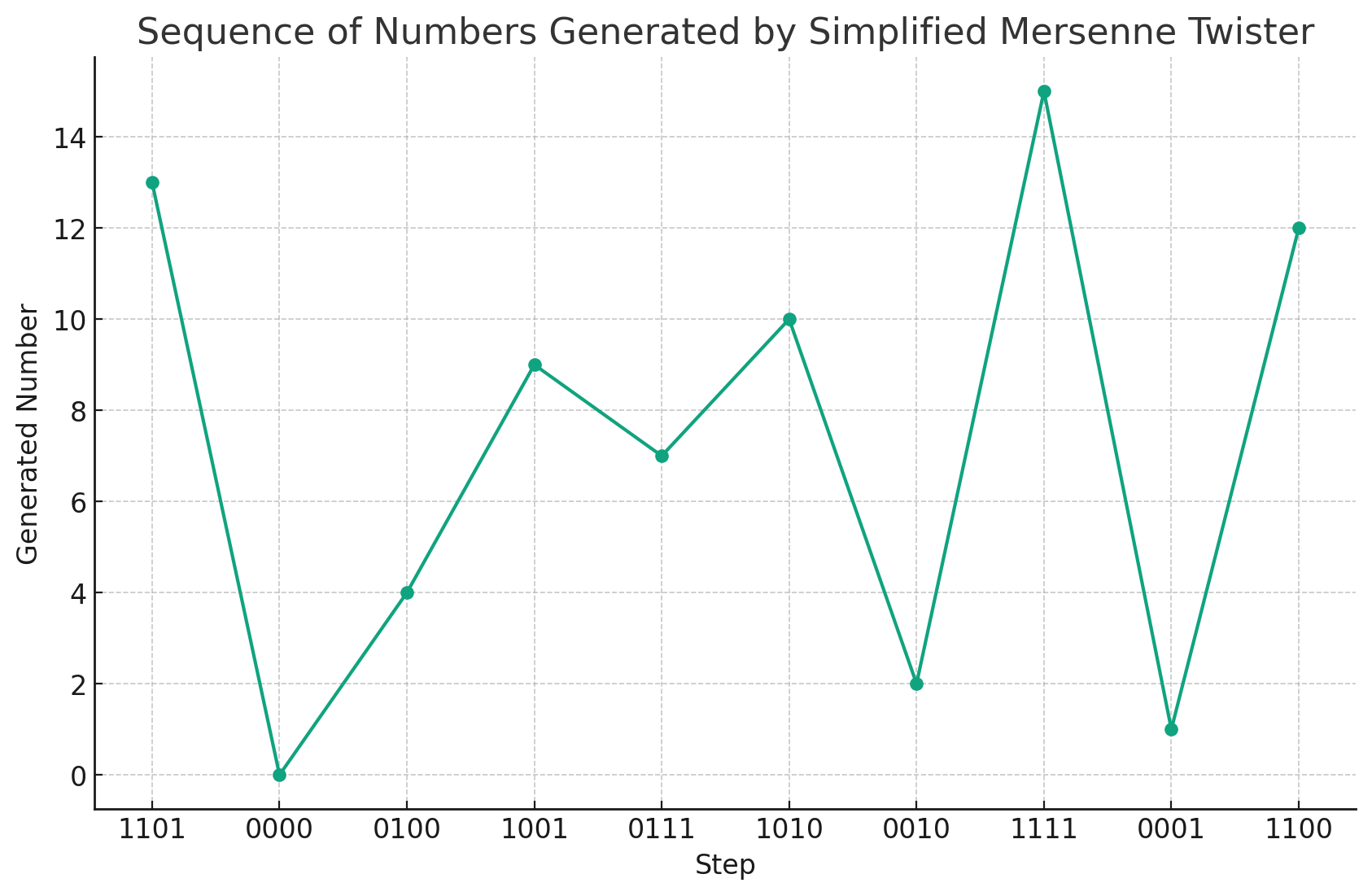
Here’s a small program that generates a sequence using this process… we can visualize the random number generation in graph and table formats.
Here’s a link to the gist for the code if you want to follow along.
| Step | Binary State | Integer Value |
|---|---|---|
| 1 | 1101 | 13 |
| 2 | 0000 | 0 |
| 3 | 0100 | 4 |
| 4 | 1001 | 9 |
| 5 | 0111 | 7 |
| 6 | 1010 | 10 |
| 7 | 0010 | 2 |
| 8 | 1111 | 15 |
| 9 | 0001 | 1 |
| 10 | 1100 | 12 |
lumber 🪵
How do you measure randomness?
Thinking about measuring randomness is an intriguing question. How would one even go about this? It might be a good point to now do the most random thing you can think of and brainstorm a bit.
There are two famous tests for randomness: the spectral test and the k-Distribution test. The spectral test is quite clever – imagine paring tuples of randomly generated points on the hyperplane. If the numbers are random, no clusters are formed. This test finds out how evenly these points fill in the space. The k-distribution test targets a similar property, but looks at the bits of a number. For each combination of a length of k bits in w-bit numbers, it checks if there is an equal frequency of each combination. In other words, if k=2, we expect 00, 10, 01, and 11 to occur with about equal frequency.
Key benefits
- Long period
- The period of a Mersenne twister is based on a Mersenne prime, which is a prime of the form \( 2^p-1 \). MT19937 has a period of \( 2^{19937}-1 \).
- A long period means generating every combination of bits in defined word size before repeating.
- High-Dimensional Equidistribution
- Efficiency and Uniformity
Why primes?
The question of old: why primes? Primes just pop up everywhere – gopher style. There were two main understandable reasons to use primes.
-
Simplify Primitivity Check
Polynomial is primitive over the binary field if the sequence generated by the linear recurrence it defines reaches maximal length before repeating.
-
Efficient Computations
Mersenne primes take the binary form of 1111… for example \( 2^5-1 \) = 31 = 11111 in binary. This makes the modulo operator easier since the overflow bits can be added back to the lower bits versus actually dividing and figuring out the remainder for non-Mersenne primes.