Intro
My brother was telling me that they were learning about tries in his data structures class. When he first told me this, I was suprised that he was pronouncing “trees” in such an odd way, but learned in fact that tries are actually a subcategory of trees.
B -> A -> S -> I -> C -> S of Tries
A trie is a type of k-ary search tree used for representing a set such that elements of the set can be looked up in an efficient manner. The most common use case is for string lookups. In the case of strings, each edge is usually represented by a character so that if you need to look up the word “cat”, then you would traverse depth first, following the edges “c”, “a”, “t”. In cases like this, an image is wayyy more informative than a description:
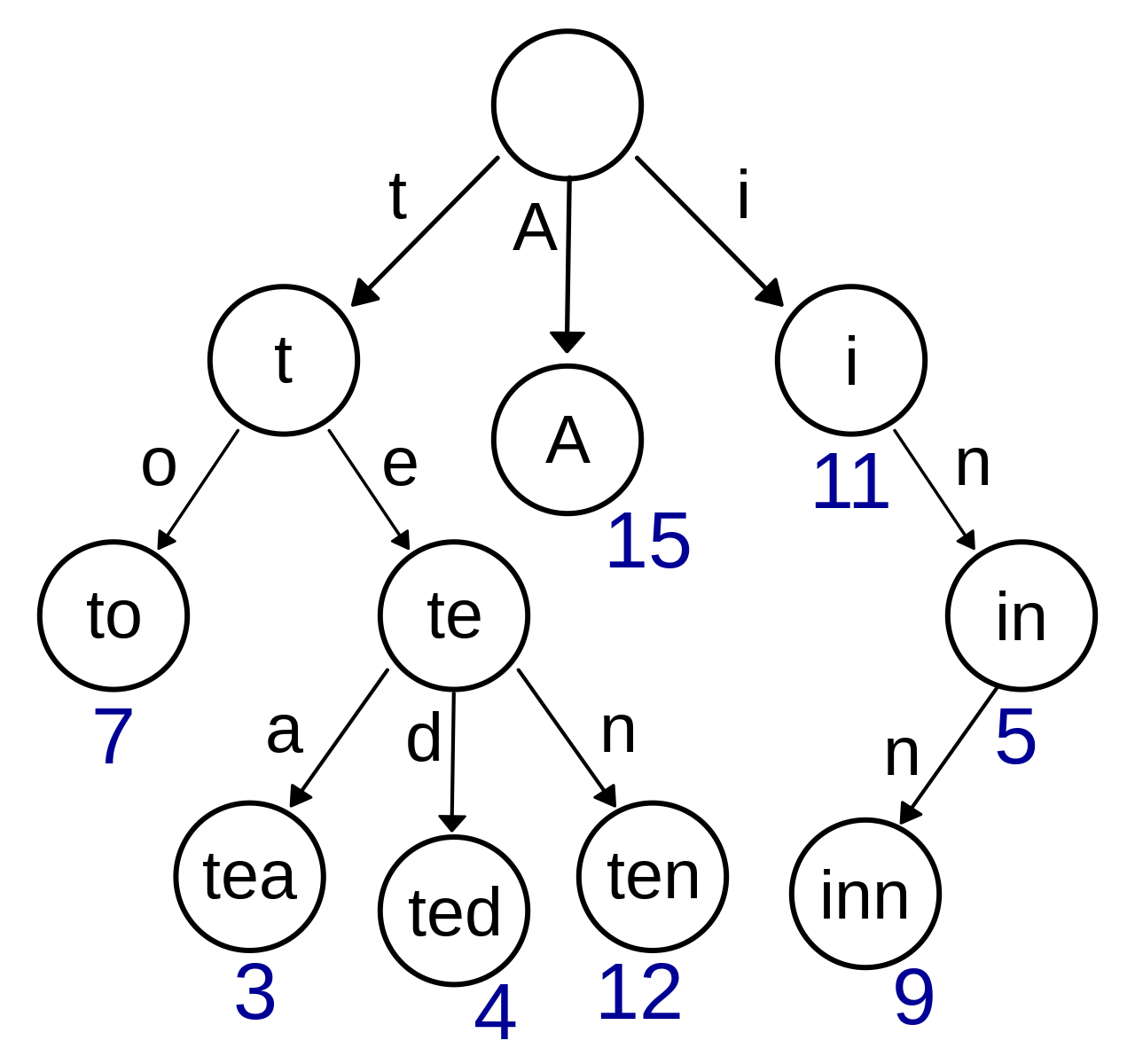
Implementing a Trie
It’s been a while since I’ve implemented a datastructure from scratch and its the same grounding feeling as walking outside barefoot. The simple C++ trie’s code is linked below:
Why Trie?
Like most datastructures, tries are versatile and many different types of data can be stored in them. However, tries are most fitting for data that share prefixes since only the nodes after the prefix need to be added for words that share a prefix with a string that is already in the set.
Time & Space Complexity
| Complexity | Trie | Binary Search Tree (BST) |
|---|---|---|
| Search | O(m) - Where ‘m’ is the key length | O(log n) - On average |
| O(n) - Worst-case (unbalanced) | ||
| Insertion | O(m) | O(log n) - On average |
| O(n) - Worst-case (unbalanced) | ||
| Deletion | O(m) | O(log n) - On average |
| O(n) - Worst-case (unbalanced) | ||
| Space Complexity | O(ALPHABET_SIZE * m * n) | O(n) - In a balanced BST |
Common Use Cases
- Autocomplete
- Internet Routing (IP address prefixes)
Natural Language Analysis with Tries
Once the trie was implemented, it was time to brainstorm what types of data could be stored in the datastructure to perhaps gain some intuition about the data itself. At first, I was thinking along the lines of genome sequences and taxonomy, since both of these seem to be categories which could have long, shared prefixes. While these could still be cool to give a trie, I reverted to the bread and butter of tries: strings.
Question: How many nodes do tries have in different languages? Put another way, what languages share the most prefixes?
I found a github repository with the top 1000 most common words in a bunch of different languages. Now, I cheated a bit (a lot) and got rid of letters that did not fit in the English alphabet. Better things to do would be to both modify the structure of the Trie and maybe phonetically translate different scripts to English characters. As it was, I just tested two languages: Aafricans and English. All of the words from the text file were inserted in a trie and the number of nodes were calculated. The conclusion from this trial was not all that interesting…
Aafricans – Number of nodes: 12696
English – Number of nodes: 12864
So I guess Aafricans (only the top 1000 words) can be represented more concisely using a trie data structure.
Conclusions & Confusions
While the results were not very impressive or insightful from this particular experiment, it was fun to be able to learn more about this datastructure and think through what it could tell you about a set. In addition to being ways to store data, datastructures can give you insights about data – how much it can be compressed, how easily it can be searched, etc.
Which sentence contains more information?
- It is sunny in LA.
- It is icy in in LA.
In information theory, the amount of information something contains is typically linked to the probability of it occurring. When parsing the meaning of these sentences, it seems that the second sentence contains more information. Since it is usually sunny in LA, this provides less information than it being icy in LA. However, if we inserted each word in the sentence in a trie, the first sentence would be longer and more “incompressable”. Upon second thought, I suppose it more about context than this singular example. If we took the forecast for three days…
It is sunny + It is sunny + It is sunny It is icy + It is sunny + It is sunny
Then once again, the second is more incompressable in both a datastructure representation and contains more information in its meaning as well.